基础
机器学习的本质就是我们通过一些已知数据训练出一个模型,然后用它来预测未知数据。
或者说,我们现在有一些数据
我们希望通过这些数据训练出一个函数:
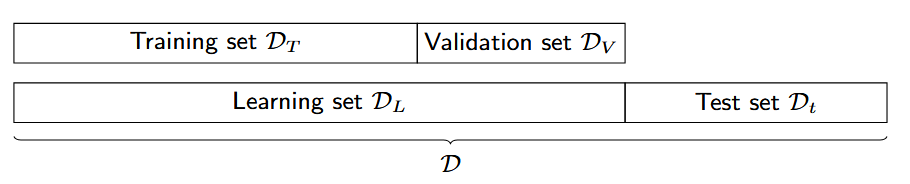
我们一般会这样划分数据:

我们会先设置一些超参数,然后利用Training set来训练这些参数对应的模型,并用Validation set来测试这些对数对应模型的准确度,最后挑选一个表现最好的,去测试Test set。
Decision Tree 决策树
来看一个例子:
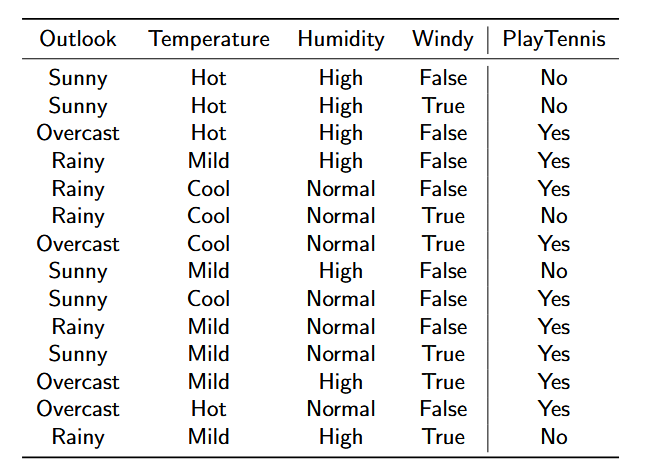
很自然的,我们会想到,通过前面3列内容的结果来推导出他们最后是否会来打网球。那么我们就可以进行一个类似二分查找的计算:
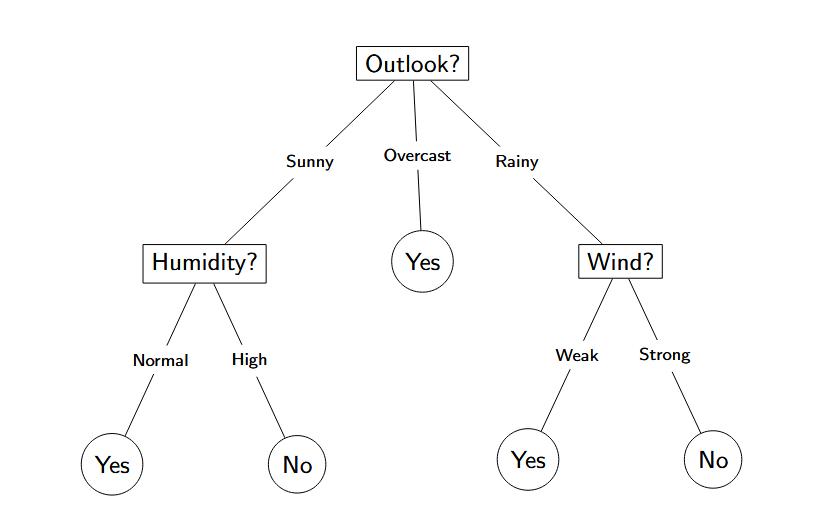
而这个就是决策树。我们会通过一系列决策来判决(预测)最后的结果。
当然,我们也可以拓展到一般的多维空间:
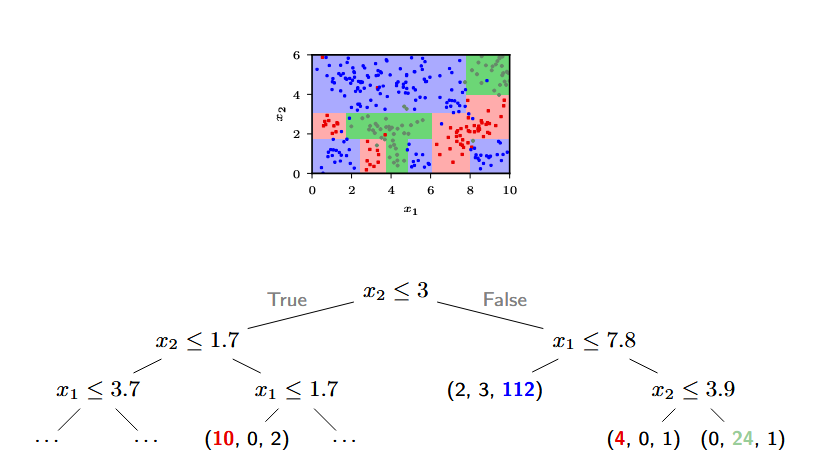
在这种决策树的图中:
- 节点(Node)表示各种决策(feature test)
- 分支(Branch)表示决策结果
- 叶子节点(Leaf)表示一部分输入空间,以及这部分空间的样品分布
分类/预测
而给一个新的点进行分类/预测也就很简单了:
假设一个新的点x通过这个决策树的各种决策最后落到了一个(代表区域$R$的)叶子节点上,而这个叶子节点的分布是$n_R = (n_{c_1,R},…, n_{c_k,R})$,而$C = \{ c_1, …, c_k\}$ 代表的是各种可能的label(分类)。那么我们只需要看当前这个区域哪种类的点最多,就可以给x也分到这个类。
数学一点的写法:
记
那么我们就给x分类成/预测成
优化/生成
我们可以通过定义不同的不纯度(Impurity measures)来判断是否要继续生成子树 (记$\pi_c = p(y=c | t)$):
- Misclassification rate
- Entropy(熵)
- Gini Index
Misclassification rate
当misclassification rate
可以得到优化时我们才会继续细分(split)节点$t$。
而针对不同的细分(split)策略$s$(把$t$分成$t_R$和$t_L$)时,我们定义所谓的优化程度(improvement):
其中$p_L$指的是$|t_L| / |t|$。
停止
可以笼统地概括成2种:
- Pre-prunning
- Post-prunning
Pre-prunning 预剪枝
就是生成的过程中判断是否停止,常见的判断条件:
- 节点纯:$i(t)=0$
- 达到最大深度
- 分支样本数太少(阈值 $t_n$)
- 分裂收益太小:$\Delta i(s,t) < t_\Delta$
- 验证集准确率不再提升
Post-prunning 后剪枝
先生成一个全面复杂的树,然后再修剪它:尝试把其中一颗子树替换成一片叶子节点(删掉 $t$ 的所有子孙,只保留 $t$(得到 $T\setminus T_t$)),然后验证错误率是否有变化。最后选择让验证误差下降最多的剪枝点。
K-Nearest Neighbours(KNN) K-近邻
KNN的核心思路其实很简单:物以类聚,人以群分。
就是假设我们有一个未知label的点x,我们查看离它最近的几个点都是什么label,如果最近的几个点都是A,那么我们也给x判定成A。
1-NN
- 定义一个距离的测度
- 计算找出离x点最近的点
- 这个点是什么label我们就给x划分成是什么label
k-NN
普通的:
设$\mathcal{N}_k(x)$为向量 $x$ 的 $k$ 个最近邻的集合,那么在分类任务中:
权重版:
设$\mathcal{N}_k(x)$为向量 $x$ 的 $k$ 个最近邻的集合,那么在分类任务中:
其中 $Z = \sum_{i \in \mathcal{N}_k(x)} \frac{1}{d(x, x_i)}$ 是归一化常数,$d(x, x_i)$ 是 $x$ 和 $x_i$ 之间的距离度量。但常数系数对求arg max没有影响,可以忽略。
注意到,每个近邻的权重$\frac{1}{d(x, x_i)}$是不一样的,距离越近的权重越高。
线性回归:
设$\mathcal{N}_k(x)$为向量 $x$ 的 $k$ 个最近邻的集合,那么:
其中 $Z = \sum_{i \in \mathcal{N}_k(x)} \frac{1}{d(x, x_i)}$ 是归一化常数,$d(x, x_i)$ 是 $x$ 和 $x_i$ 之间的距离度量。
如何选择k
k这种参数被称作超参数,是事先给定的,用来控制学习过程的参数。
超参数调优过程 (Hyper-parameter tuning procedure):
- 使用 训练集 训练模型(在 KNN 中即存储数据)。
- 在 验证集 上评估不同 $k$ 值的性能,并挑选出最好的 $k$。
- 在 测试集 上报告最终的性能。
但是当维度升上去了,knn会变得及其复杂,需要大量的内存。




